課題5:Running Coupling Strengthsを計算する
home , 準備
(linux | editor | X window | ROOT | login | remote ROOT | Geant4) , 課題(1 | 2 | 3 | 4 | 5
| 6)updated 2011.11.21a
[1] 概 要
標準モデルの三つの力は相互作用エネルギーとともに変化する。電磁気相互作用 U(1)EM やハイパーチャージ対称性 U(1)Y の力は screening 効果の減少で強くなる(説明)。反対にQCD の SU(3)C と自発的対称性の破れる前の Electro-weak の SU(2)L の力は、エネルギーとともに anti-screening 効果の減少で弱くなる(説明)。力の強さを示す coupling strengths α3, α2, α1 の変化は RGE (renomalization group equation)に従って変化する。
ヒッグス粒子が予想どおりに100~1000GeVで発見されれば標準理論が完成する。しかしヒッグス粒子の筆量補正にまつわる階層性問題が存在する。これを解決するに大きく分けて2つのシナリオがある:
- 超対称性粒子が1 TeV付近に存在する。中性の超対称性粒子は暗黒物質は有力候補である。
- 余剰次元モデルでは重力が短距離で強くなる。
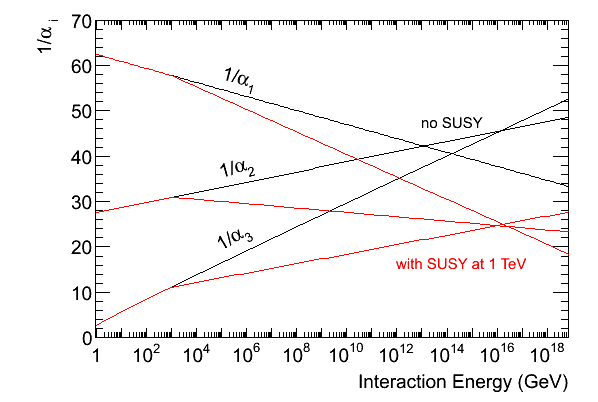
大統一理論:q = mZ でのデータ値から出発し、超対称性粒子が 1 TeV 付近に存在する場合は、3つの coupling strengths は 1016 GeV付近で1点に交わり、大統一が起こることを示唆している。ここでは Amaldi et al., Phys. Lett. 260(1991)447(とその要約) に従って coupling strengths の running を計算してプロットする。
[2] 走る結合定数を計算しプロットする
- 論文に従ってプログラム running_alpha.cc を作成する。どうもその論文の式(15)の係数が 1/2πではなく1/4πらしいので、そこだけ変えてある。
- g++ running_alpha.cc でコンパイルする。./a.exe > nosusy.dat で実行し、出力を nosusy.dat に出す。
- root でマクロplot_nosusy.Cでnosusy.dat を読み込んでこのようにプロットする。3つの結合定数は1点で交わらないことが分かる。
- running_alpha.ccの中の変数 SUSY(SUSY粒子が存在する質量領域)を1000 GeVに変更し、コンパイル後 ./a.exe > susy.datでSUSY粒子が1 TeV付近に存在する場合を計算する。
- 提出課題5a:plot_nosusy.Cを発展させてnosusy.datとsusy.datの両方を読み込んで重ねるマクロをつくりプロットする。図のようなプロットが得られるはず。
- 提出課題5b:ヒッグスダブレットが2個存在する(ヒッグス粒子の数は5個))場合を計算しプロットする。
