課題１：パイオンからニュートリノビームを作る

home , 準備 （linux | editor | X window | ROOT | login | remote ROOT | Geant4） , 課題（1 | 2 | 3 | 4 | 5 | 6）updated 2011.11.19a

[1] 概要

  • 素粒子実験の一つにニュートリノ実験がある。J-PARCでは加速した陽子を炭素標的に当てて多量のパイオンを作り出し、荷電パイオンから崩壊してできたニュートリノを295km離れた神岡（Super Kamiokande測定器, SK）に向けて送り、ニュートリノ振動実験T2Kを行っている。
  • off-angleビームの使用：T2K概要図に示すように、SK測定器は親粒子のパイオンの飛ぶ方向に対して2.5°の角度の位置にある。こうするとニュートリノのエネルギーを1 GeV付近に調整できる。
  • ここではパイオン崩壊を相対論的に扱い、ニュートリノのエネルギー分布を計算しグラフにプロットする。

    [2] パイオンの崩壊過程 π→μ+νμ をプログラムする

    1. パイオン（pion）は π+,π0,π-の３種類がある。このうちπ+,π-は質量が139.57MeV、寿命が2.6×10-8secであり、99.99%は  π→μ+c  の崩壊をする。（註：素粒子の質量などの最新情報はPDG( Particle Data Group)が毎年まとめている。例えばπの性質はこの表にまとめられている。)
    2. 簡単のために標的で作られた π+ の運動量は 20 GeV とし、Z軸に沿って走っているとする。
    3. 実験室系でのπ, μ, νμ の４元運動量をそれぞれ q=(q0,qx,qy,qz), a=(a0,ax,ay,az), b=(b0,bx,by,bz) とする。重心系では q*, a*, b* とする。
    4. エネルギー・運動量の保存則から重心系でのμ,νμの運動量をこの様に計算する。
    5. ローレンツ変換して実験室系でのμ,νμの運動量を計算するプログラムpiDecay.cxxを作る。
    6. コンパイル(g++ piDecay.cxx)・実行(./a.exe)してこのような結果がでることを確かめる。
    7. ただし、このプログラムの中では重心系でmuonが出る方向の角度（天頂角θ,方位角φ)を一様にランダムサンプルしているが、これは間違いで、位相空間（phase space）に従ってd(cosθ)dφでサンプルすべきであった。次のpimu_1.cxxでは直してある。

    [3] 20 GeVのパイオンからのニュートリノのエネルギー分布を求める

    1. π→μ+νμ崩壊プログラムをfunctionを使ったプログラム pimu_1.cxx に変更してpionとニュートリノのエネルギーを出力するようにする。
    2. g++でコンパイル後 ./a.exe > pimu_1.txt で出力をpimu_1.txtに保存する。
    3. pimu_1.txt を読み込んでヒストグラム/プロットするROOTマクロ plot_pimu_1.C を作る。
    4. ROOTを開き .x plot_pimu_1.C でプロットすると右図の分布が出る。
      注：パイオン崩壊から作られるミューオンもニュートリノもエネルギー分布がフラットである。また質量の重い粒子（ミューオン）に殆どのエネルギーが移っていることがわかる。これらは二体崩壊の典型的な特徴である。
    5. 提出課題1a：20GeVのK±のμν崩壊から発生するμとνμのエネルギー分布の図を作れ。なおK±の質量はPDG表（上記）に載っている。νμ分布は青色で示すこと。
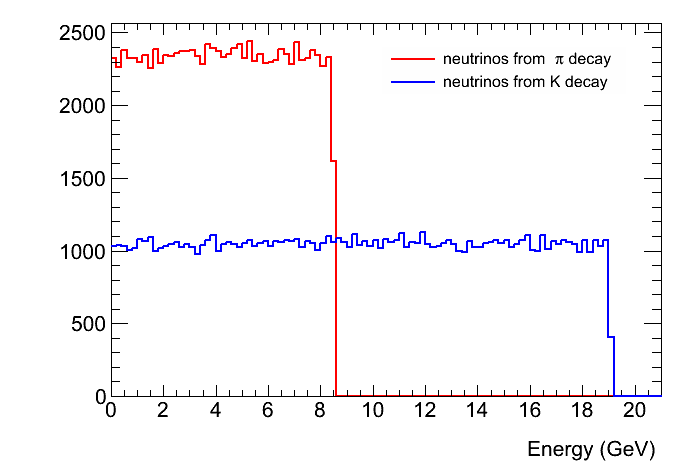
    6. この結果を利用して20GeVのπ+とK+が同数できたしたときのνμのエネルギー分布を比較するプロットを重ね合せ法 h->Draw("SAME") を 使って作ると右図のようになる。高いエネルギーのνμは殆どKからできていることが示されているが、これは親粒子と子粒子の質量差の違いに起因するものである。
    7. この比較図の作成に使ったマクロの例 plot_piKnu.C には大変便利な TLegend というクラスを使っている。TLegendの使用に慣れておくことを勧める。

    [4] パイオンの飛行距離分布

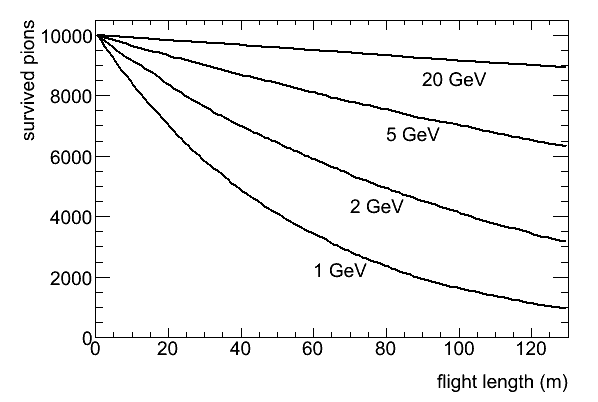    静止しているパイオンは2.6×10-8秒で崩壊する。エネルギーが高くなり速くなると固有時間の進みがSQRT(1-β2)=1/γ倍だけ遅れγ倍寿命が長くなりそれだけ崩壊しにくくなる。これを見るためにROOTのマクロを作ってパイオンの飛ぶ距離分布を計算しプロットする。
    1. ROOTマクロファイルpion_flight.C（2 GeVの場合）をコピーし、ROOT上で.x pion_flight.Cと実行してこのような図を作る。
    2. pionのエネルギーを1, 5, 20 GeV と変えて再計算し、プロットをh->Draw("SAME");を使って重ね合わせると、右図のようになることを示せ。

    [5] ニュートリノのエネルギー分布

    1. [3]で使ったプログラム pimu_1.cxx を以下のように修正して pimu_2.cxx を作る：
      1. 標的で作られたpionのエネルギー分布は1-20 GeVで一様とする（現実と異なるが計算を簡単にするため）。
      2. pionはビーム軸(z方向）に沿って進む（これも計算を簡単にするため）。
      3. decayトンネルの長さは130mとする。
      （ヒント：修正例）
    2. pimu_2.cxx をコンパイル・実行して、decayトンネル内で崩壊した粒子のの情報を pimu_2.txt に書き出す。
    3. ROOTのマクロを使ってプロットするとpimu_2.pngが得られる。
    4. pionのビーム軸から2-3°(35-53 mrad）の範囲にあるニュートリノのエネルギーを書き出すプログラム pimu_3.cxx を作り、コンパイル・実行してpimu_3.txtに書き出す。
    5. ROOTマクロ plot_enu.Cでプロットすると右図のニュートリノのエネルギー分布がニュートリノ振動の実験に都合のよい 0.7 GeV 付近に限定されることがわかる。
    6. しかし現実により近い発生pionのエネルギー分布は一様ではなく、低いエネルギーのpionがより多く発生する。エネルギー分布を例えば 1/E4 であるように乱数発生させる方法として、関数を積分して得た頻度分布を0-1乱数で実現するやり方がありこの記述を参考にする。
    7. 一様分布と1/E4分布を比較するROOTマクロ plot_pion_gen.Cで、伏せた部分（XXXXXXXX,YYYYYYYYY）を正しく入れて実行すれば右図ができるはずである。
    8. 提出課題1b：pionのエネルギー分布を1-20GeVの間で E-4 分布で発生させる。簡単のためにpionはビーム軸に沿って発生するとする。130mのdecayトンネルで作られるνμのエネルギー分布を、角度制限ない場合とビーム軸から2-3°に制限した場合 に求めてプロットする。