Rapidity（ラピディティ）yとPseudorapidity h の定義と性質
・粒子のRapidity yは正式には longitudinal rapidity と呼び
で定義される。ここで
である。この変数y は粒子の縦方向と横方向を分離して記述するのに便利で、粒子の質量に関わらず
が成り立ち、したがって粒子のPhase
Space
がrapidity yに比例することがわかる。z方向のLorentz 変換（g=coshD, b=tanhD）に対しては
となり、rapidityの値は定数 D の差に帰する。粒子がとりうる最大のrapidityは、重心系でEmax=
だから
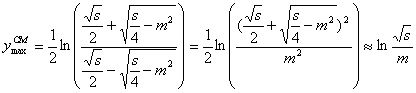
となり粒子によってy のkinematical limit がちがう。
・粒子の種類（質量）が分からないときは pseudorapidity h を使う．y の定義式に m=0を入れて
で与えられる．ここでθは粒子の発生角度（天頂角）である。コライダー実験ではこの h が頻繁に使われる。この式から逆にθは
で与えられる。この式を使えばrapidityと角度の関係がすぐ計算できて
|
pseudorapidity h |
polar angle θ |
πの本当のrapidity y |
||
|
p=1 GeV/c |
10 GeV/c |
100 GeV/c |
||
|
0 |
90° |
0.00 |
0.000 |
0.000 |
|
1 |
40.395° |
0.983 |
1.000 |
1.000 |
|
2 |
15.415° |
1.883 |
1.999 |
2.000 |
|
3 |
5.700° |
2.459 |
2.990 |
3.000 |
|
4 |
2.099° |
2.633 |
3.932 |
3.999 |
|
5 |
0.772° |
2.662 |
4.635 |
4.995 |
|
-1 |
139.605° |
-0.983 |
-1.000 |
-1.000 |
|
-2 |
164.585° |
-1.883 |
-1.999 |
-2.000 |
|
-5 |
179.228° |
-2.662 |
-4.635 |
-4.995 |
となる。粒子の質量がノンゼロの場合は、rapidityとpseudorapidityに違いが出てくる。一例としてpion（質量0.1397 GeV/c2）の場合の本当のrapidity y の値を表に載せた。
図１．アトラス測定器中心部断面図とプソイドラピディティ h
LHCでの陽子陽子衝突で発生するpionなどの軽い粒子のpseudorapidity の分布は、 h =-3〜3でほぼ平らであり、rapirityあたり6個ほどの粒子が発生する。実際、Pythia６を使って14TeVの陽子陽子衝突で発生する荷電粒子の分布を取ってみると、図2のようなラピディティ分布になる。重い粒子（例えばHiggs粒子）は h =0付近のみ分布する。
（2003.4.26 T. Kondo記）